From Vector to Function — Transformations, Basis, and Kernel Method
Here is only some superficial thought about Fourier transformation (and other similar transformations), space basis, and kernel method. I will continuously update the post for new thoughts.
1. What is function
A function is an infinite vector. Every thought begins here. As the following figure shows
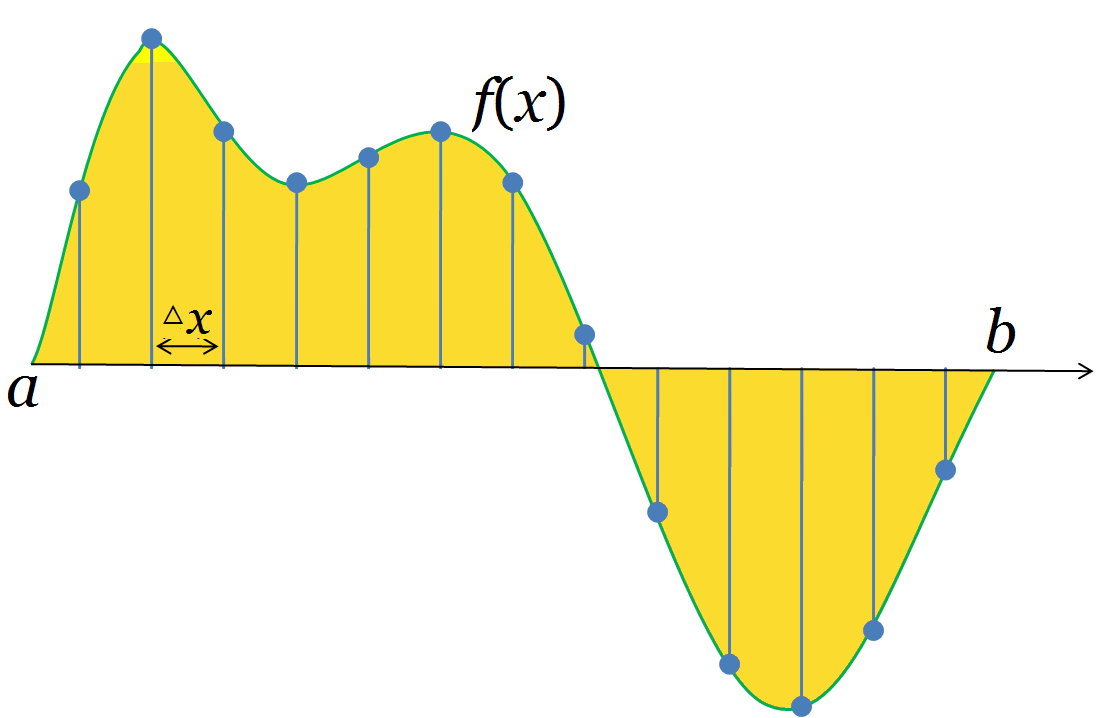 p>For a function defined on the interval , we take samples by an interval . If we sample the function at points , then we can transform the function into a vector . When , the vector should be more and more close to the function and at last, it becomes infinite.
p>For a function defined on the interval , we take samples by an interval . If we sample the function at points , then we can transform the function into a vector . When , the vector should be more and more close to the function and at last, it becomes infinite.
The above analysis assumes to be a real number. But when is a vector, it still holds. From now on, we use bold font such as to denote normal vector in space; use to denote the function itself, namely the infinite vector; use to denote the evaluation of the function at point . And the evaluation of a function should be a real number.
2. Function inner product
Vectors have inner product. For vector and , the inner product of and is defined as
Similarly, functions have inner product. For two functions and sampling by interval , the inner product may be defined as
at first thought. However, the above equation doesn't converge when . Something is missing. As approaches 0, the dimension of and grows larger in our denotation.
For a vector, the dimension is discrete. We only have the first, second,... dimension. But we don't have the 0.5, 1.5,... dimension. When we transform a function into a vector, every sample point is located at a discrete dimension. However, this should not be true, since the dimension of each sample point should be stable so that the above equation will converge. Therefore, the dimension is not discrete for functions, but continuous. What we miss is the difference between adjacent dimensions for normalization. Therefore, we can define the inner product of two functions as
3. Basis
What is the meaning of inner product? For two vectors and , the inner product is the projection of one vector to the other.
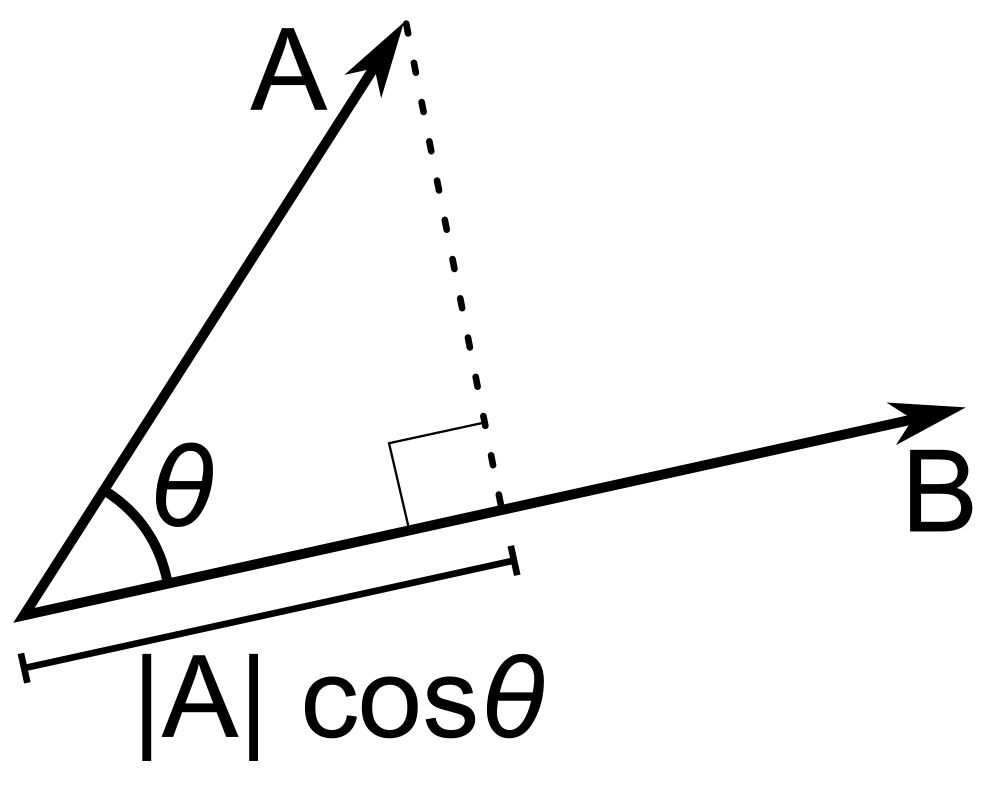
Namely
If we regard the length of as one unit, then the inner product is the coordinate of the projection on . Therefore, given a set of orthogonal basis vector where and . The basis vectors can establish a space by linear operations. Any vector in the space can be denoted as
More generally, if , then
Functions also have basis, which can be orthogonal or non-orthogonal. If we define the set of function basis, any function in the space can also be decomposed into the combination of several basis functions. Function inner product can also be used to calculate the coefficient on any specific basis. However, since the dimension of function is continuous, there may be infinite basis functions.
For a set of function basis , if and , any function within the space can be denoted as
If ,
similar to the vector case.
4. Example: Transformations
Let the basis functions is interger) be
defined on interval . Here I use to index the basis functions in order to distinguish from the imaginary number . These construct a space and any function defined on interval is within the space. It can be proven that any two basis function are orthogonal (for complex numbers, the latter term should take conjugate transpose when calculating the inner product).
where and . The "length" of basis is
If a function defined on interval is within the space, it can be written as
And the coefficient can be calculated as
Actually this is the Fourier series. A more thorough discussion about Fourier series can be found here.
5. Kernel Function
Instead of , we use to index the basis function. Let
The set of basis functions can be denoted as one function with two parameters. In the example, is discrete. However, this is not the full space. If we let to be real number, then any functions may be represented.
The function is kernel function. It may be viewed as a cluster of basis functions. If they are orthogonal for any , and the squared "length" of basis , any function can be represented as
And the coefficient of a function on a basis is calculated as
Therefore, kernel function is able to transform a function into another space (a function space).
6. Example: Transformations
Let the kernel function to be
where is the imaginary number. It is easy to show that the basis functions are mutual orthogonal,
when . Then squared "length" of basis is
This constitutes a full function space. The coefficient is calculated as
The original function is represented as
Actually this is the Fourier transformation. Other transformations such as Laplace transformation, Z-transformation are similar. Maybe wavelet is also within the framework.
7. Something about Kernel Method
For a kernel function , if we regard it as a cluster of basis, then we can get a space by the linear combination of the basis. However, the basis may not be orthogonal. This is somewhat like a matrix , if we use the columns of to generate a space. To construct orthogonal basis for the space, we can use eigen value and eigen vectors of . Similarly, we can use eigenfunctions as the basis for the function space generated by . If all the eigen values are positive, then the kernel function is positive. If the inner product is defined as
This is the reproducing kernel Hilbert space. It is commonly used to calculate the inner product of two mappings in a high-dimension feature space. When linear model is not enough, we can map the points into feature space and use kernel trick to calculate inner product. Support Vector Machine is an example.